あまりのあるわり算が苦手
例えば、12÷4の計算をするときに4の段の九九で12になるものを見つければよいと機械的に暗記しているだけで、÷という記号(演算子)が「○個ずつ分ける(包含除)」や「○人に等しく分ける(等分除)」という操作イメージと結びついていない場合、13÷4わり算の計算の問題を出すと、4の段の九九で13になるものがないから、できないということになり混乱してしまいます。
具体的な支援の方法
step1 具体物にによる支援
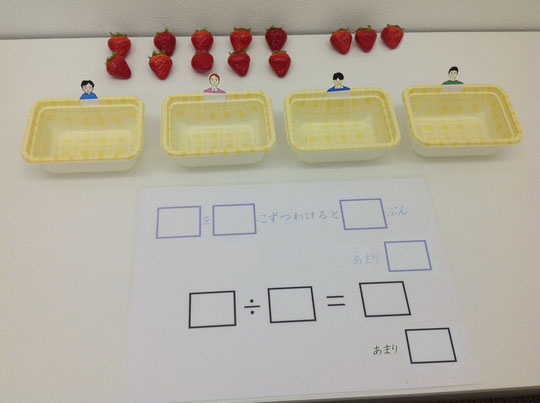
写真1のように、具体物と分けるための容器を準備します。「イチゴが12個あるね。4個ずつ配ってみるね。」と声かけし、4個ずつイチゴを容器に分けていきます。3人目まで配るとイチゴが全部なくなって、3人にイチゴを配ることができることが分かります。その後に算数シート①に「12こを4こずつわけると3人ぶん」になるように数字を入れていきます。包含除のわり算の考え方がしっかりと分かるためにはこのプロセスが重要になります。数を変えていろんな場合について同じ数ずつ分けることを子どもにしてもらいます。

しっかりと文章で操作を表わすことができるようになったところで『「12こを4こずつにわけると3人ぶん」を算数で表すと「12÷4=3」になります。』と声かけをし、算数シート②(写真2)に数字を入れていきます。いろん状態の問題を作り、子どもに答えを書いてもらいます。

次に、配る元になるイチゴの数を13個にして、「イチゴが13個あるね。4個ずつ配ってみるね。」と声をかけ4個ずつイチゴを容器に分けていきます。4人目の人に分けようと思ってもイチゴが1個しかあまっていなくて、4人目の人には、イチゴを4個分けることができないことが分かります。「3人に分けることができて、イチゴが1個あまるよね。」と声をかけ、算数シート③に「13こを4こずつわけると3人ぶん あまり1こ」になるように数字を入れ、「算数で表すと13÷4=3あまり1と書きます。」と言いて式を完成させます。あまりのあるわり算の考え方がしっかりと分かるためにはこのプロセスが重要になります。数を変えていろんなあまりのある場合についての課題を子どもにしてもらいます。
step2 具体物を使ったわり算の計算の仕方の意味把握の支援
配る元になるイチゴの数を13個に戻して、「『イチゴ13個を4個ずつ配ると何人に分けることができ、何個あまるか。』計算で求めてみますね。」と言ってから算数シート④(写真4)に「13÷4」まで書き入れます。
つぎに、1人目の容器に4個イチゴを入れ、1回目で4個配ります。「4個を1人に配ったから配ったイチゴの数は4×1=4で4個」「次いくよ」といって2回目に入ります。「4個を2人に配ったから配ったイチゴの数は全部で4×2=8で8個」「まだイチゴが残っているね。」「次いくよ」といって3回目に入ります。「4個を3人に配ったから配ったイチゴの数は全部で4×3=12で12個」「4人目の人にイチゴを配ろうと思ってもイチゴが1個しかないので4個配ることはできないよね。」と言ってから「13÷4の計算の答えは、4の段の九九で13を越えないものをみつければいいね。」と伝え、「しいちがし・しにがはち・しさんじゅうに・ししじゅうろく、ししまでいくと13を越えるので答えは3というふうに答えを出します。」とまとめます。
「あまりは、配る元の数13から実際に配った数12を引いて1になるね。」と計算の仕方を確認し、算数シートに答えを書き入れます。


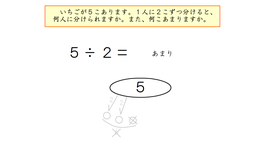
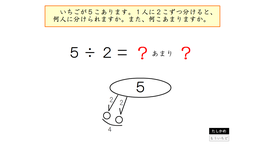
step3 支援ソフト「あまりのあるわり算の計算のしかた」による支援
さんすうベーシックプラスさんすう3「あまりのあるわりざん」の中の『あまりのあるわり算の計算のしかた』の課題(図1・図2・図3)を繰り返しおこなうことにより、あまりのあるわり算の計算の仕方を定着させていきます。
 「はる先生の
さんすう教室」
「はる先生の
さんすう教室」